View on GitHub

GE-Kempten.github.io

Inoffizieller Wiki des Studiengangs Informatik Game Engineering and der Hochschule Kempten

Einführung in die Informatik

Kompetenzen

Inhalte

Einführung

Die Informatik ist die Wissenschaft der automatischen Verarbeitung von Informationen, insbesondere mit Hilfe von Digitalrechnern. Der Begriff setzt sich aus „Information“ und „Automatik“ Sie ist eine interdisziplinäre Wissenschaft mit Wurzeln im Elektroingenieurwesen und in der Mathematik und ist in folgende Teilbereiche unterteilt:

Geschichte der Datenverarbeitung

Konstruktion von Rechenhilfen und mechanischen Rechenmaschinen

Bau digitaler mechanischer Rechenmaschinen (Zahnräder zur Ausführung arithmetischer Operationen)

Elektronische mechanische Rechenmaschinen

Elektronische Rechenmaschinen mit Relais oder Elektronenröhren

Grundbegriffe der Informatik

Information

Information ist eine Mitteilung, die sich aus einer Räumichen oder Zeitlichen Folge physikalischer Signale zusammensetzt, die beim Empfänger ein bestimmtes Verhalten bewirkt und Kenntnis über bestimmte Sachverhalte und Vorgänge in einem Teil der wahrgenommenen Realität vermittelt. Information ist immateriell und kann nur in Form von Daten im Rechner verarbeitet werden.

Daten stellen Informationen zum Zweck der Verarbeitung anhand bekannter oder unterstellter Abmachungen dar. Sie sind die physikalische Repräsentation von Information. Dabei wird die Information codiert und muss zur Verarbeitung decodiert werden.

Die Codierung beschreibt die Art der Repräsentation von Information zur Datenverarbeitung. Mögliche Anforderung an eine Codierung sind Kompakte Darstellung um die Dateigröße zu verringern oder Redundanz um Übertragungssicherheit zu gewährleisten.

Eine Nachricht ist eine Folge von Zeichen, die von einem Sender ausgehend in der Form von Daten an einen Empfänger übermittelt wird.

Codierungstheorie

(Binär-)Codierung): Festlegung einer Abbildungvorschrift -> bestimmter Art von Information und bestimmtes Mustern aus Nullen und Einsen

Eigenschaften

Aber: Nicht alle Anforderungen können gleichzeitig erfüllt werden

=> Entscheidung des Codes durch Anwendungszweck

Informationsgehalt

Informationsgehalt/Entscheidungsinformation eines Zeichens (in bit):

-> Auftretungswahrscheinlichkeit des Zeichens

-> minimaler Anzahl von 0/1-Entscheidungen $$

Entropie bzw. mittlerer Informationsgehalt :

Mittlere Wortlänge einer Codierung:

-> Wortlänge des Codes des i-ten Zeichens

Shannon’sches Codierungstheorem:

wenn = -> Codierung kompakt

Code Redundanz:

Größe der Anteil einer Nachricht, die im statistischen Sinne keine Information trägt

Umsetzung

Darstellung von:

Logische Werte

Name Schreibweise
Negation
Konjunktion
Disjunktion

Polyadische Zahlensysteme

Polyadische Zahlensysteme unterscheiden sich in erster Linie durch ihre Basis, also durch die Anzahl der verwendeten Symbole.

nicht-polyadische Zahlensysteme sind z.B. gemischte Zahlen und römische Zahlen.

Natürliche Zahlen

Allgemein Darstellung (natürlichen Zahlen, polyadische Zahlensysteme):

Arithmetische Operationen funktionieren genauso wie im Dezimalsystem

Addition

Multiplikation

Umrechnung

Potenzrechnung

Die n-te Stelle der Ziffer wird auf Basis des Zahlensystems (Anzahl an möglichen Werten) potenziert und anschließend mit dem Wert der Stelle multipliziert.

Ergebnis: Dezimalzahl

32 + 8 + 2 =

42

3328 + 160 + 11 =

3499

Horner-Schema

B = Basis des Zahlensystems (z.B. Hexadezimal: 16)

b = Umwandelnde Ziffern; n = Stelle der Ziffer

Ergebnis: Dezimalzahl

Beispiel 1: in Dezimal

Beispiel 2: in Dezimal

Sukzessive Division

Wir nehmen eine beliebige Zahl und teilen diese durch die Basis des gewünschten Systems. Das Ergebnis wird ohne Kommazahl genommen (nicht Runden!) und der Rest neben dran geschrieben. Wenn das Ergebnis 0 erreicht, dann werden die Reste rückwärts aneinandergereiht.

n = Umwandelbare Zahl

B = Basis des Zielzahlensystems

q = Ergebnis ohne Rest (bzw. ohne Komma)

b = Reste

Anschließend die Reste (b) rückwärts zusammenzählen

Ergebnis: Zahlensystem von B

Beispiel 1: Umwandlungs von nach Binär/Dual

R 1

R 0

R 0

R 1

R 1

R 1

R 0

R 0

R 1

R 0

R 1

Beispiel 2: Umwandlung von nach Hexadezimal

R D

Tipp: 32*16 = 512 -> 525 - 512 = 13 bzw. D

R 0

R 2

Sukzessive Multiplikation:

“Braucht niemand” - Jeb 2017

Vereinfachtes Schema:
  1. Umrechnung ins Binärsystem
  2. Aufteilung jeder Ziffer in ein Block
  3. Umwandlung in Zahlensystem anhand Anzahl der Blöcke (2er Potenzen):
    • Oktal: 3 Blöcke ( = 8)
    • Hexadezimal: 4 Blöcke ( = 16)

Vereinfachtes Schema

Vorteil: Schnellere und kürzere Umrechnung

Nachteil: Nur Umwandlung zwischen 2er Potenzen möglich

Ganze Zahlen

Bis hier können wir aber nur positive Zahlen darstellen. Folglich werden verschiedene Arten genannt, wie unser Zahlenbereich dargestellt werden kann.

Die simpleste Art ist die Vorzeichendarstellung. Dabei entscheidet das 1. Bit - also das ganz links - über das Vorzeichen.

Darstellung

Anwendung bei Datentyp float.

Nachteile:

Um diese Nachteile zu lösen wurde das Zweierkompliment entwickelt.

Nehme wir beispielweise 4 Bit wodruch wir Zahlen darstellen können. Wir zählen nun von 0000 (0) rauf, bis wir die Obergrenze 0111 (7) erreicht haben. Nun fangen wir bei 1111 (-1) an rückwärts zu zählen und enden bei 1000 (-8).

Darstellbarer Bereich: bis

Der erste Nachteil ist gelöst - 0 (0000) ist nun einmal verfügbar. Und Rechnen?

Kümmern wir uns erstmal um die Umwandlung einer positiven Zahl zum negativen Konterpart und andersrum:

  1. bitweise Negation
  2. Addition von 1

Umwandlung

Jetzt können wir Rechnen. Zur Errinnerung:

Beispiel:

bitweise Negation

Information 1. bit -> Minus, also

Anwendung: Datentyp signed int

Spezielfall:

0 komplimentiert ist immer noch 0, da alle Bits zu 1 werden und anschließend die Addition von 1 alle wieder umdreht.

Eine dritte Darstellungsmöglichkeit ist die Verschiebung des Zahlenbereichs ins Positive (= Addition Bias). Dabei wird ein Bias festgelegt, welcher auf alle Zahlen draufaddiert wird. Dieser kann beispielweise durch den maximalen Wertebereich definiert werden (z.B. 2^4 = [-128, 127]).

Beispiel:

Bias: 7 = 0000 0111 + BIAS = 1000 0110 -7 = 1111 1001 + BIAS = 0111 1000

Anwendung: Exponentialdarstellung

Nachteil: - Muss bekannt sein, dass jetzt das Bias-Verfahren angewendet wird. - Wenn Bias nicht mehr bekannt, dann weiß man nicht mehr die Zahl

Reelle Zahlen

Festpunktdarstellung: Komma immer an vorher festgelegter Stelle

Bsp: Finanzbereich: EUR in ct, d.h. Verschiebung um 2 Kommastellen

Gewünschter Wert = 192,27 (analog: €)

Gespeichert wird: (analog: ct)

Zurückwandeln: und

Gleitpunktdarstellung: Fest Anzahl von Bits für Vorzeichen (V), Exponent(E) ud Mantisse (M)

Genormte Formate (IEEE):

  • Short Real: V (1bit), E(8bit), Mantisse (23 bit)
  • Long Real: V(1bit), E(11bit), Mantisse (52 bit)

Vorgehen am Beispiel 18,4:

  1. Umwandlung des vorderen Teils (vor Komma):

R 0

R 1

R 0

R 0

§§ 1 : 2 = 0,5$$ R 1

=> 10010

  1. Umwandlung des hinteren Teils (hinter Komma):

R 0

R 1

R 1

R 0

R 0

R 1

=> 0110011001100110011001100…

  1. Normalisieren | Verschiebung des Kommas

=> Exponent: 4

  1. Charakteristik = Exponent + Bias

Bias = 127

=>

  1. Vorzeichen

+ -> 0

- -> 1

  1. Gleitkommzahl

V = 0 (1 bit)

E = 10000011 (8 bit)

M = 00100110011001100110011 (23 bit)

Einzelzeichen

ASCII: American Standard Code for Information Interchange

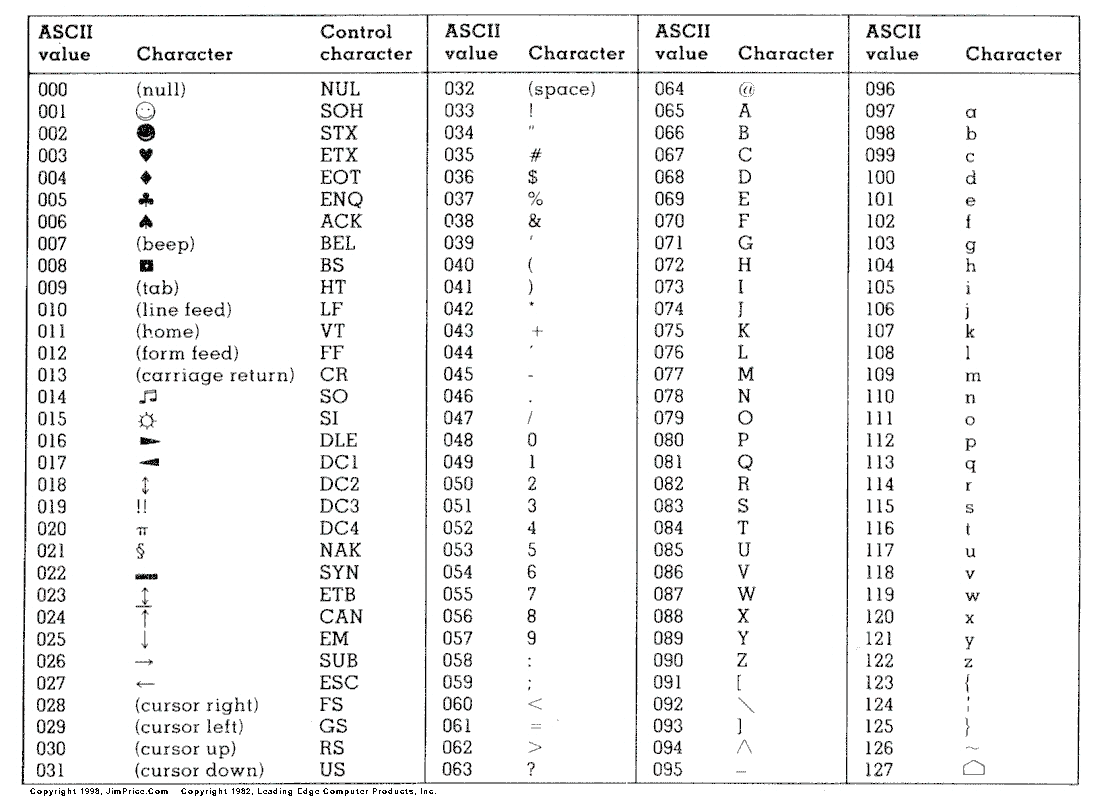
ASCII

Erweiterung

UTF-8

Unicode-Zeichen werden eine Byte-Kette mit variabler Länge zugeordnet.

Dadurch soll Kompatibilität mit bisherigen Zeichensätzen erreicht werden und in Zukunft im Internet den ASCII-Standard und HMTL-Sonderzeichen ablösen.

Code-Zuordnung:

Bsp. Unicode UTF-8
1. 0000 0000 - 0000 007F 0xxx xxxx
2. 0000 0080 - 0000 07FF 110x xxxx 10xx xxxx
3. 0000 0800 - 0000 FFFF 1110 xxxx 10xx xxxx 10xx xxxx
4. 0001 0000 - 0010 FFFF 1111 10xx 10xx xxxx 10xx xxxx 10xx xxxx

zu 1.: Höchstens Bit 0, restliche Bits entsprechen ASCII Code.

ab 2.: Die x enthalten die Bitkombination des Unicode-Zeichens (rechtsbündig aufgefüllt), die Anzahl der 1en- zu Beginn steht für die Anzahl der Bytes.

Softwarelösung

Die Informaitk beschäftigt sich damit, für ein Problem der reallen Welt eine effektive Lösung durch Einsatz von informationsverarbeitenden Systeme zu finden.

Dabei hat sich folgende Vorgehensweise eingebürgert:

Kann jedes Problem durch einen Algorithmus beschrieben und gelöst werden? => Logik- und Berechenbarkeitstheorie

Formulierung des Algorithmus des Programms - Wie muss eine formelle Sprache aussehen? => Theorie der Programmiersprachen

Kann der Computer ein Programm - also den Algorithmus - ausführen? => Komplexitätstheorie

Spezifikation

=> vollständige, detaillierte, unmissverständliche und widerspruchsfreie Problembeschreibung

Eigenschaften

Vollständigkeit: Alle Anforderungen und relevanten Vorraussetzungen/Rahmenbedinungen sind angegebene

Detailliertheit: Alle zur Lösung zugelassenen Hilfsmittel sind erwähnt

Unmissverständlichkeit: klare Kriterien, wann eine Lösung zulässig ist - klare Anforderungen, die auf unterschiedliche Weise interpretiert werden können

Widerspruchsfreiheit: keine miteinander unverträglichen Anforderungen

Inhalt

Standardzustand:

Zielzustand:

Rahmenbedingungen: zulässige Operationen

Beschreibungsformen

Umgangssprache + “Wortschatz” aus dem Anwendungsbereich

formale Sprache + “Wortschatz” aus dem Anwendungsbereich + Regeln

Vor- und Nachbedingungen

Formulierung von logischen Bedingungen umgangssprachlich oder formal. Ergebnis ist entweder true oder false.

Pre: relevante Eigenschaften, die vor Beginn der Problemlösung gelten müssen

Post: relevante Eigenschaften, die nach Abschluss der Problemlösung gelten sollen

Beispiel: größter gemieinsamer Teiler (ggT)

Pre P: M, N sind ganze Zahlen mit 0 < M, N < 32768 ()

Post Q: Z = ggT(M, N) d.h. Z ist ein Teiler (Zahl ohne Rest) von M, N und für jede Zahl Z’, die auch M, N teilt, gilt Z’ ≤ Z

Zwischen {P} und {Q} findet dann ein Ablauf ab.

komplexe Problemstellungen

Viele Einzelanforderungen:

Viele unterschiedliche Beteiligte:

systematische Ermittlung und Behandlung von Anforderungen bei komplexen Problemen => Requirement Engineering

Algorithmus

Ein Algorithmus ist eine vollständige, eindeutige, und explizite Vorschrift zur schrittweisen Lösung eines Problems.

Ausgangszustand -> Algorithmus -> Zielzustand

Bsp: Eine Kochanleitung ist auch ein Algorithmus

Bestandteile
Aufbau
Anwendung in der Informatik

Ausführorgan ist der Computer, welche Algorithmen nur in einer computerverständlichen Formulierung versteht. Diese Formulierung muss unabhängig von Rechner/Programmiersprache sein.

Objekte können oft nicht direkt durch den Compiter beeinflusst werden.

Eigenschaften

Plicht:

Optional:

Darstellung

Algorithmen werden i.d.R. durch eine der 3 folgenden Formen dargestellt:

Beispiel hier wird der ggT sein. Der Algorithmus bzw. Ablauf A befindet sich zwischen {P} A {Q}.

Flussdiagramm / Programmablauf (DIN 66001)

Flussdiagramm - Allgemein

Vorteile:

Nachteile:

Beispiel: Größter gemeinsamer Teiler (ggT)

ggT - FD

M = 6, N = 8

N = 8 - 6 = 2

M = 6 - 2 = 4

M = 4 - 2 = 2

M = N = Z

Struktogramm / Nassi-Shneidermann-Diagramm

Beschreibung der Einzelschritte in Strukturblöcken. Verschachtelung und Wiederholungen möglich.

Struktogramm - Allgemein

Beispiel: ggT

ggT - SD

Pseudo-Code

Nutzung von programmiersprachlichen Grundelementen in Kombination mit eigenen Anmerkungen.

Zuweisung: -> oder =

Verzweigung: IF Bedingung THEN … ELSE … END

Wiederholung: WHILE Bedingung DO … END

Überprüfung der Bedingung vor dem Ausführen

Wiederholung: REPEAT … UNTIL Bedingung

Überprüfung der Bedingung nach dem Ausführen

Beispiel: ggT

Lese 2 Zahlen M und N ein
WHILE M != N
	DO
	IF M > N
	 	THEN M = M - N
		ELSE N = N - M
	END
END
Z = M

In der C++-Programmierung kann der Pseudo-Code mit Kommentaren verwirklicht werden.

Entwurf

Eine systematische Vorgehensweise ist notwendig, da i.d.R. die Entwicklung eines Algorithmus nachvollziehbar und Arbeitsteilung möglich sein soll.

Entwurfsprinzipien sind allgemein gültige, universell einsetzbare und anerkannte Konzepte und Richtlinien des Entwurfs, z.B. Schrittweise Verfeinerung, Modularisierung und Strukturierung.

Entwurfstechniken sind im speziellen Fall anwendbare Verfahren und Vorgehensweisen für den Entwurf.

Top-Down-Entwurf / Schrittweise Verfeinerung
  1. Entwurf eines groben Algorithmus | abstrakte Operationen, manipulierte Objekte
  2. Verfeierung des 1. Schritts
  3. Wiederholung des 2. Schritts bis der Algorithmus nur noch aus elementaren Operationen des Ausführungsorgans besteht

Durch die Verfeinerung werden gleichzeitig auch Operationen, Ablaufstrukturen und Datenstrukturen verfeinert.

Beispiel: Eine Folge von Werten soll nach ≤ sortiert werden. soll das Element an der Position i bereichnen.

Version 1

Sortiere (w_1, w_2, ... w_n)

Version 2.1

Initialsiere w_1 mit a_1
i = 2
WHILE Element w_i noch nicht einsortert AND i <= n
DO füge w_1 an der richtigen Position a_1 ... a_i ein
i = i+1
END

Version 2.2

a_1 = w_1
i = 2
WHILE i <= n
DO j = i-1
	WHILE (j != 0) AND (w_i < a_j)
	DO j = j-1
	END
	füge w_i an (j+1)-ter Position in a_1 ... a_n ein
	i = i + 1
END

Version 3

a_1 = w_1
i = 2
WHILE i <= n
DO j = i-1
	WHILE (j != 0) AND (w_i < a_j)
	DO a_j+1 = a_j
	j = j-1
	END
	a_j+1 = w_i
	i = i + 1
END

Zusätzlich ist eine schrittweise Vergröberung bzw. der Bottom-Up-Ansatz möglich. Dabei werden Lösungen von Teilproblemen zu größeren Einheiten zusammengefasst. Diese Vorgehensweise ist i.d.R. weniger zielgerichtet.

z.B. arithmetische Operationen: zuerst einfach Operationen (Addition, Subtraktion), dann Bilden komplexer Operationen bis zu Matrizenrechnung, numerische Integration.

Modularisierung

Zerlegung von Problemen in Teilprobleme. Teillösungen entsprechen dann sog. Modulen.

Prinzip: Aufteilung des Problems in folgende Schritte:

  1. Klare Abgrenzung unabhängiger Teilprobleme
  2. Weitgehend voneinander unabhängige Teilprobleme
  3. Getrennt bearbeitbare Teilprobleme
  4. Lösungen ohne Beeinträchtigung von anderen Teilproblemen gegen Alternativ-Lösungen austauschen

Vorteile:

Strategien zur Modulbildung:

Strukturierung

Prinzip: sinnvolle Darstellung der logischen Eigenschaften von Daten, Abläufen und Verdeutlichung der Zusammenhänge.

Rekursion

Rekursion ist die Rückführung eines Problems auf einfacherer Exemplare desselben Problems.

Rekursive Problemlösung:

  1. Originalproblem wird in einfachere Exemplare desselben Problems zerlegt (Teilprobleme)
  2. Lösung der Teilprobleme
  3. Zusammensetzen der Lösung des Ausgangsproblems aus den Lösungen der Teilprobleme

Vorraussetzung für rekursive Lösung: irgendwann müssen bei Zerlegung Teilprobleme entstehen, die sich ohne weitere Rekursion direkt lösen.

Bestimmte Formen rekursiver Probleme lassen sich einfach nicht-rekursiv (iterativ) lösen.

Rekursive Algorithmus sind oft eleganter und kürzer als nicht-rekursiver, aber nicht zwangsläufig effizienter!

Beispiel: Fakultät n! = n * (n-1)

fak(n) =
IF n < 2
	THEN return 1
	ELSE return n * fak(n-1)
END

Programmiersprachen

Nach der Spezifikation und Algorithmisierung eines Problems der realer Welt können nun die Anweisungen an den Computer übermittelt werden - Programm. Damit dies aber möglich wird, muss dem Computer erklärt werden, wie er das Programm lesen muss - Programmiersprache.

Programmiersprachen -> Spezialfall algorithmische Sprachen -> Spezial formale Sprachen

Formale Sprachen: Eine formale Sprache L ist eine Teilmenge einer Menge T*

Aber:

Arten von Sprachen

Problemorientierte Sprache (Hochsprache): Formulierung von Algorithmen aus der Sicht der Probleme, welche z.T. spezifisch für einen bestimmten Problembereich sind. Die Programme sind unabhängig von Rechner-/Prozessortyp

Maschinenorientierte Sprache: maschinelle Verarbeitung von Algorithmen. Aber: Programme sind spezifisch für einen Rechner-/Prozessortyp, d.h. dies ist die Zielsprache für Compiler.

Maschinenorientierte Programmiersprachen

Maschinensprache: Anweisungen binär codiert, wodurch der Rechner/Prozessor diese direkt interpretieren kann. Das sorgt dafür, dass man das dies schwer lesbar ist. Zusätzlich ist dies schwer zu programmieren, da Interna des Rechners/Prozessors sowie die Darstellung aller Informationen exakt bekannt sein müssen. Auérdem sind nur einfache Operatonen möglich.

Zusätzlich gibt es noch eine optionale Schicht namens Mikroprogramme in welcher Maschinenbefehle interpretiert werden, d.h. Elementaraktionen. Diese Schicht ist für den Programmierer nicht frei zugänglich.

Assembler-Sprache: Anweisungen haben gleiche oder ähnliche Struktur wie Befehlswörter eines bestimmten Rechner-/Prozessortyps. Durch die Nutzung von mnemotechnischen Abkürzungen wird die Programmierung angenehmer.

Umsetzung: Assembler | ADD -> Assembilierung -> Maschinensprache | 1001 1100

Compiler und Interpreter

Wie man von oben entnehmen kann, ist die Programmierung durch eine Maschinenorientierte Programmiersprache komplizierter, wodurch man eher auf Problemorientierte Programmiersprachen ausweichen möchte. Trotzdem muss diese noch für den Prozessor umformuliert werden. Dazu gibt es 2 Mittel:

Compiler: Übersetzt den Programmtext der Quellsprache in eine Zielsprache, d.h. in die Maschinensprache. Vor Ausführung wird das Maschinenprogramm im Hauptspeicher durch ein spezielles Ladeprogramm bereit gestellt.

Quellprogramm (Eingabe) -> Compiler -> Zielprogramm (Ausgabe)

Interpreter: Übersetzung und Ausführung den Programmtext schrittweise, d.h. Übersetzung und Ausführung einer Anweisung und anschließend das gleiche für die nächste Anweisung.

Quellprogramm (Eingabe) -> Interpreter -> direkte Ausführung

Umsetzung: Problemorientierte Sprache | + -> Compilierung, Interpretierung -> Maschinensprache | 1001 1100

Übersicht

Programiersprachen - Übersicht

Imperative Sprachen

Programme sind schrittweise ablaufende Folgen von Befehlen auf bestimmten Datenelementen. Die Reihenfolge der Operationen wird weitesgehend durch den Programmierer bestimmt.

Prozedurale Sprachen: explizite Beschreibung des Ablaufs innerhalb eines Programmes. Dabei sind einzelne Datenelemente als Variablen (symbolische Bezeichnung eines Speicherbereichs) ansprechbar.

Objektorientierte Sprachen: Programme sind Sammlung miteinander kommunizierende Objekte, dabei ist der innere Aufbau der Objekt nach außen hin verboren (Datenkapselung). Der Zugriff auf den inneren Zustand ist nur über vorgesehene Operationen möglich. Die Reaktion des Programmes ist dann eine Folge bestimmter Aktionen, die auch zwischen Objekten stattfinden kann. Gleicharige Objekte werden zu Klassen zusammengefasst, welche in einer Generalisierungshierachie angeordnet werden. Bestimmte Klassen bauen auf andere Klasen auf (Vererbung).

Deklarative Sprachen

Ein Problem wird auf einer Grundlage eines bestimmten mathematischen Modells formuliert. Die Programmierumgebung schreibt automatisch den konkreten Algorithmus um.

Logiksprachen: Problem wird in einer mathematische Logik als Sammlung von Fakten und Regeln formuliert. Die Programmabarbeitung entspricht dem Versuch, logische Aussagen zu beweisen oder zu widerlegen.

Funktionale Sprachen: Das Program entspricht einer mathematischen Funktion. Aufbau durch verschachtelte Anwendung aus elementaren Funktionen. Zusammensetzungmöglichkeiten sind die Kompisition (Hintereinanderausführung)zu, Fallunterscheidung und Rekursion. Aber: Rein funktionale Sprachen verfügen nicht über Wertzuweisung und Wiederholungsanweisung.

Grundelementen

Daten: Arbeitsmaterial des Programmes, dabei haben diese Daten bestimmte “Sorten”, d.h. sie kommen aus einem Datentyp/Datenstruktur, welche unterschiedlich viel Speicherplatz benötigen.

Anweisung: Befehle aus dem das Programm besteht. Die Abarbeitung erfolgt nach einer bestimmten Reihenfolge, der Kontrollstruktur.

Datentyp

ZusammenhangStandarddatentypen

Nun wissen wir, welche elementaren Datentypen es gibt. Kombiniert mit Variablen können wir nun Daten speichern.

Deklaration und Defintion

Deklaration: Einer Variable (symbolischer Name) wird ein Datentyp zugeschrieben. Dadurch kann nun genügend Speicherplatz vorbereitet werden und fehlerhafte Operationen (Typfehler) werden vor dem Übersetzen ersichtlich.

C++: datentyp variablenname

Definition Durch Nutzung der elementarsten Operation - die Zuweisung - können Variablen bestimmte Werte übergeben werden, d.h. sie werden in die dazu passende Speicherzelle eingefügt.

C++: =, Bsp. int eineVariable = 2 (Kombination aus Deklaration und Definition)

Eigene Datentypen

Neue Datentypen können erstellt werden, indem die Trägermenge beeinflusst wird. Auch hier können die Funktionen succ und pred benutzt werden.

Unterbereichstypen: Trägermenge wird durch eine vom Programmierer angegebenen Minimalwert und Maximalwert definiert.

Nicht verwendtbar in C/Java

Aufzählungstypen: Jedes Element der Trägermenge wird angegeben.

C/Java Variante: enum name {}

Datenstrukturen

Neue Datentypen können erstellt werden, indem bereits vorhandene Typen kombiniert werden. Oft haben diese neuen Datentypen neue Funktionen.

Im Folgenden werden 3 sehr praktische Datenstrukturen erklärt. Aber es gibt noch viel mehr.

Array (Feld)

Verkettung mehrere Variablen eines Datentyps. Ein Element in dieser Kette kann mit der Selektions-Funktion [] visiert werden.

C++: datentyp arrayname[größe], arrayname[position] = inhalt

Record (Verbund)

In einem Verbund können nun Elemente - meistens Variablen - verschiedener Datentypen zusammengefasst werden. Aufgrund der Teil-Ganzes-Beziehung müssen jedem Element ein Name gegeben werden, wodruch diese auch unterscheidbar werden.

C++: struct name {variablen}, Zugriff: name::eineVariable

Pointer, Reference (Zeiger, Referenzen)

Pointer: indirekter Zugriff auf die Speicherposition einer Variablen

Über die Referenzierung kann einer Variablen und somit auch der Speicheradresse ein alternative Name übergeben werden.

Mit der Deferenzierung kann man dann auf eine Referenz weisen, welche dann auf die entsprechende Variable zeigt.

C++: Pointer - *var, Reference - &var

Kontrolstrukturen

Unser Programm besteht bisher aus Operationen und Datentypen. Damit kann man aber nur simple Programme schreiben. Mit Kontrollstrukturen möchten wir Vorgaben zur Reihenfolge einbauen.

3 elementare Kontrollstrukturen: Sequenz, Alternativen, Iteration

Sequenz

Darunter versteht man eine sequentielle Aneinanderreihung bzw. eine Reihenfolge von Anweisung und deren Ausführung - Block.

C++: {Anweisung1; Anweisung2; … AnweisungN;}, ; kennzeichnet das Ende einer Anweisung

Alternativen

Durch Nutzung von Boole’schen Ausdrücken verwirklichen wir Fallunterscheidung.

Ist eine Bedingung wahr, so wird eine Anweisung ausgeführt. Ist die Bedingung falsch, so wird eine andere Anweisung ausgeführt.

C++: if(Bedingung){Anweisung} else {Anweisung}, man kann auch einen dritten Fall mit else if einbauen

Interation

sind Wiederholung von Anweisungen im sog. Schleifenrumpf, solange eine Bedingung wahr ist.

abweisende Iteration: 1. Überprüfung der Bedingung 2. Ausführung | mind. 0 Ausführung

C++: while(Bedingung){Anweisung}

nicht abweisende Iteration: 1. Ausführung 2. Überprüfen der Bedingung | mind. 1 Ausführung

C++: do {Anweisung} while (Bedingung)

Sonderfall: Zählschleife

Prinzip: Eine Schleife wird mit einer Laufvariablen versehen, welche bei jedem Durchlauf verändert wird (i.d.R. Inkrement). Sobald die Laufvariable die Bedingung nicht mehr erfüllt, bricht die Schleife ab.

C++: for(laufvariable; bedingung; inkrement); Die Laufvariable wird oft mit datentyp i oder j deklariert und definiert. Es sind auch auch Variablen von außerhalb möglich.

Unterprogramme

Wie oben bereits angemerkt, besteht unser Problem aus mehreren Teilproblemen, welche wir in Algorithmen aufgeteilt haben. Ein Weg Algorithmen in unser Programm zu integrieren sind Unterprogramme, welche aus weiteren Unterprogrammen bestehen können.

Formal ausgedrückt heißt das, dass ein Unterprogramm eine Sequenz ist, welche im Quellcode definiert ist. Über die Festlegung einer Schittstelle kann dann das Unterprogramm jederzeit aufgerufen werden.

Wir Unterscheiden zwischen einer Prozedur, primär ein Vorgang, und einer Funktion, welche ein Ergebnis liefert z.B. Addition mit dem Ergebnis Summe.

In der Schnittstelle müssen verschiedene Übergabeparameter definiert werden. Dazu wird eine Parameterliste mit Typ und Bezeichner erstellt. Die übergebenen Werte, also auch Variablen, sind dann unter dem Bezeichner wiederzugeben (formale Parameter), d.h. Wenn ich eine var1 und var2 habe, dann sind sie in der Funktion Addition unter Summand1 und Summand2 wiederzuerkennen.

Die Parameter können über zwei verschiedene Arten übergeben werden:

Call-by-Value: Bei der Übergabe werden Kopien von den Parametern erstellt, wodurch die Operationen mit den formalen Parameter nicht den Wert der originalen Parameter beeinflusst.

Vorteil: Nebeneffekte können vermieden werden

Nachteil: Aufwendigkeit, da Parameter kopiert werden. z.B. Bei einer Kopie von einem 3D-Modell

C++: Standard

Call-by-Reference: Bei der Übergabe werden Verweise die Parameter erstellt, d.h. bei Operationen mit formalen Parametern ändert sich auch die Werte der übergebenen Parameter.

Vorteil: Weniger Rechenaufwand

Nachteil: ungewollte Nebeneffekte können entstehen

C++: Nachstellung über Pointer

Bei Aufruf eines Unterprogrammes wird eine laufende Sequenz unterbrochen, dann zum Anfang des Unterprogrammes gesprungen und diese ausgeführt und anschließend die unterbrochene Sequenz fortgeführt. Dadurch können Unterprogramme beliebig oft aufgerufen werden und sogar weiter Verschachtelt werden.

C: **datentypDesRückgabewertes name (Parameterliste){…}; Nutzung von void wenn kein Rückgabewert erwünscht ist.

Objektorientierte Programmierung

Problem ist, dass Unterprogramme öfters bestimmte Datenstrukturen benötigen und zugleich diese auch nur bestimmte Operationen zulassen. Indem man Unterprogramme und Datenstrukturen vereint, können Überprüfungen von zulässigen Operationen bei der Übersetzung möglich gemacht werden und es können Zugriffsrechte für interne Datenstrukturen mit eigens definierten Funktionen möglich gemacht werden.

object: gekapselte Strukten in Form von abstraken Datentypen. Besitzen Datenkomponenten oder verwendbare Funktionen.

class: Beschreibung des Aufbau von Objekten in einem Schema. Legt Typ des Objektes fest.

C++: class Name {Zugriffsrechte}; Zugriffsrechte: public, protected, private

Elementare Algorithmen

Elemenatre Datensturkturen

Autometentheorie, Sprachen und Compiler

Grundlagen der Softwareentwicklung